Neural networks (also referred to as connectionist systems) are a computational approach, which is based on a large collection of neural units (AKA artificial neurons), loosely modelling the way a biological brain solves problems with large clusters of biological neurons connected by axons. – Wikipedia

{% excerpt %} In essence Neural networks are digital representations of their biological counterparts, and while that sounds intimidating – unless you have a strong background in statistics or cognitive science – NN are not that complicated once you understand the individual building blocks for a Neural Net. {% endexcerpt %}

For illustration purposes let’s take a look at the simplest possible Neural Network, the perceptron:

The perceptron is a computational model of a single neuron, and as we can see it consists of 3 basic neural nodes, each of the with a unique function:

• Inputs: Also referred to as sensors are in charge of communicating with either software or hardware and passing signals(data) to the Neural network, for example data sources in the case of software or a webcam in the case of hardware.
• Neurons: A basic unit of computation, it takes input from other nodes(sensors) and computes and output.
• Output: Also referred to as actuators, allow our NN to interact with its environment, outputs can be hardware or software, for example return a true or false value or activating a stepper motor.

Layers

Each node type will be typically arranged in a single layer, with the exception of Neurons which can have many more layers, to clarify let’s take a look at a more complex Neural Network type, a Feed-Forward Neural Network:

The input and output layers are self-explanatory, but what is a hidden layer?

Hidden Layers

The hidden layer(s) is the collection of one or more layers of artificial neurons that are in charge of doing the computation, transforming the inputs into something the output layer can use. In order to understand what happens inside this hidden layer, we need to first understand the concept of emergence:

In philosophy, systems theory, science, and art, emergence is a phenomenon whereby larger entities arise through interactions among smaller or simpler entities such that the larger entities exhibit properties the smaller/simpler entities do not exhibit. – Wikipedia

Each hidden layer neuron has an internal mechanism that governs if the neuron becomes active and sends a signal of its own to the next layer – which can be another hidden layer or the output layer itself.

If we want to break it down, we can then say that a Neural network takes one or more inputs, performs some sort of computation and returns a value – often in the form a vector – that can be used for further processing.

How Neurons Make Decisions

In order to understand how neurons compute the input values and in turn make decisions – aka return an output – we need to add two more elements to our neural network understanding.

• Connections: The individual connections between each node (inputs, neurons, outputs).
• Connection Weights: Each individual weight represents the strength of the connections between nodes. Another way of thinking about it is how much each ‘neuron’ cares about a particular input value.

With those two new components let’s review our original perceptron diagram:

Alright, now that we have expanded our knowledge about how neurons are connected let’s take a look at how they make a decision based on their inputs.

The Activation Function

Each neuron will take all the connected inputs with their corresponding weights and apply what is called an activation function and return a single output value.

Now, here is where we could start going into the mathematics behind neural networks; but as promise but for now we wont; all we need to know is that there are a number of common activation functions that can be used with Neural networks. To mention a few:

• Step Function
• Sigmoid
• Linear
• Gaussian

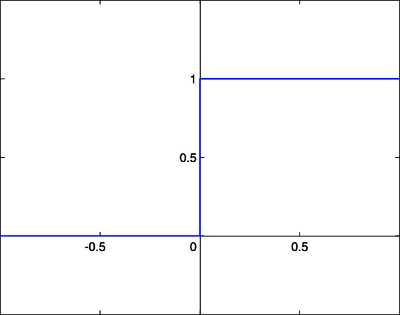
In the case of our perceptron will be using a step function, will return one of two values 0 (OFF) or 1 (ON), this means our neuron will always a binary value – that is, the neuron is either firing or not, and the graph representation of that function looks something like this:

Putting it all together

Let’s quickly put all we learned together and write a simple perceptron:

This python perceptron is doing a couple of things we haven’t covered yet, like training, and adjusting the connection weights based on the error. For now, the only important thing to understand is that our perceptron takes 3 inputs, applies a step function to such values and attempts to predict the output value.

Running the perceptron will return something like this:

Training Perceptron for 1000 iterations
Starting weights: [ 0.90185083  0.75965753  0.10658775]
.......................................................
Training completed
Weights after training: [ 0.90185083  0.35965753 -0.49341225]
Running trained Network against Test Data
[0 0 0]: 0.0 -> 0
[0 1 0]: 0.359657525652 -> 1
[1 1 1]: 0.768096100245 -> 1
[0 0 1]: -0.49341225179 -> 0
[1 0 0]: 0.901850826383 -> 1

The result

Can you spot the pattern that the Neural Network is supposed to predict? Leave a comment if you think you figure out the pattern and how well our perceptron did.

Summary

We covered a lot of content in this second post of the series and we now have a much better understanding of the individual elements in neural networks, next we are going to cover ANN topology or how to put organize and connect all of our Neurons.